'모두의 딥러닝' 개정 2판 + 세종대학교 최유경 교수님의 인공지능 강의(2021) + alpha 로 공부한 글입니다.
# 딥러닝의 동작 원리
# 3장: 선형 회귀(Linear regression)
딥러닝의 가장 기본적인 계산 원리 두 가지는 선형 회귀와 로지스틱 회귀입니다. 그럼 우선 선형 회귀에 대해 공부해봅시다.
# 3.1 선형 회귀(linear regression)의 정의
'y는 x에 따라 달라진다.'고 할 때, x를 독립 변수라 하고 y를 종속 변수라고 합니다. 독립 변수는 독립적으로 변할 수 있는 값이고 종속 변수는 독립 변수에 따라 종속적으로 변하는 값입니다.
ex. x시간을 공부하면 y점이 나온다.
선형 회귀는 독립 변수인 x를 사용해 종속 변수 y의 움직임을 예측하는 작업입니다. 특히 선형인 모양으로 시스템을 추정하고 그 모델을 바탕으로 미래를 예측하는 것을 말하죠. 이때 선형은 비선형과 반대되는 말로, 일차함수로 나타낼 수 있습니다.
하나의 x 값으로 y 값을 설명할 수 있는 경우를 단순 선형 회귀(simple linear regression)라고 하고, x 값이 여러 개 필요하여 x1, x2, x3 등의 값을 사용하는 경우를 다중 선형 회귀(multiple linear regression)라고 합니다. 그렇지만 두 경우 다 종속 변수인 y 값이 하나인 것은 동일합니다. 실제로 현실에서 일어나는 대부분의 일은 여러 개의 독립 변수를 가질 수밖에 없으므로 다중 선형 회귀가 많이 사용되며, 일반적으로 선형 회귀는 다중 선형 회귀를 나타낸다고 합니다.
# 3.2 단순 선형(simple linear regression) 회귀
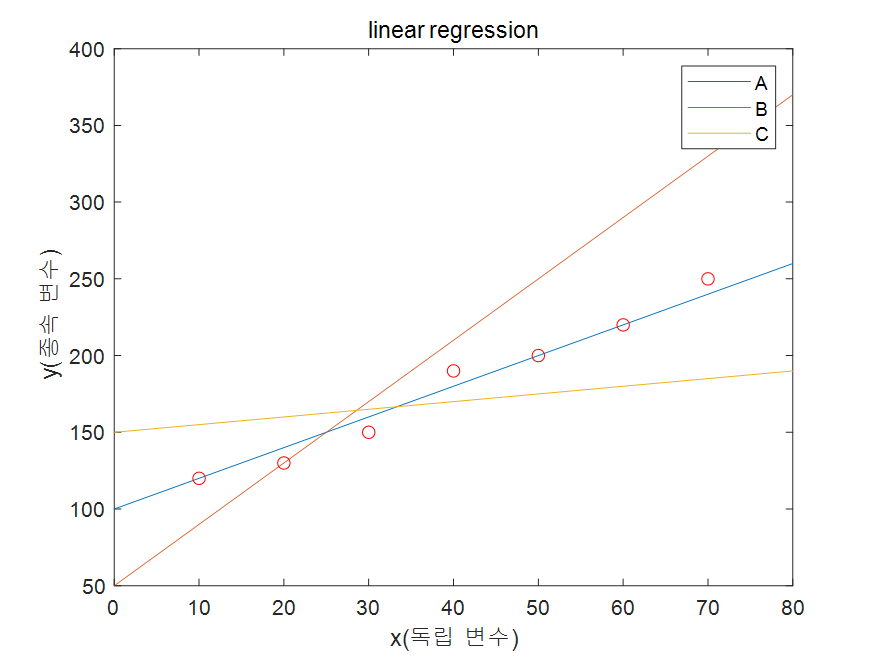
매트랩을 이용하여 선형 회귀 함수를 그려 보았습니다. 참고로 코드는 아래와 같이 작성했습니다.
x = [0;10;80];
y1 = 2*x+100;
y2 = 4*x+50;
y3 = 1/2*x+150;
plot(x,y1)
hold on
plot(x,y2)
hold on
plot(x,y3)
hold on
xlabel('x(독립 변수)')
ylabel('y(종속 변수)')
title('linear regression')
ys=[120 130 150 190 200 220 250];
for x = 10:10:70
scatter(x,ys(fix(x/10)),'red')
end
legend({'A','B','C'})A, B, C 세 개의 일차 함수와 scatter 점을 찍어보았는데요, 이 중에 점들의 선형 회귀 그래프는 어떤 것일까요? 사실 직감으로 감이 오실 것 같습니다. 바로 A 그래프죠.
그럼 왜 A 그래프인가요? 어떤 기준인가요? 좀 더 확실하게 수식화할 수 있도록 이야기 해보면 바로 이것일 겁니다.
'함수의 답과 정답의 차이가 작은 그래프'
이 함수의 답과 정답의 차이를 바로 'cost function'이라고 하고 이는 'loss function', 'objective function'과 혼용되어 쓰입니다. 예측된 값(함수)를 H(x)=Wx+b라고 가설을 설정하고 정답(참값, GT, Ground Truth)을 y라고 하면 cost = H(x) - y로 나타낼 수 있습니다. 이 경우에 모델 파라미터는 W와 b가 됩니다. 예측 함수는 가설 설정에 따라 바뀔 수 있습니다.
그럼 이제 전체적인 cost가 가장 작은 그래프를 찾으면 그게 가장 적절하게 예측된 그래프라고 볼 수 있겠죠? 그 그래프를 찾는 방법은 이렇습니다. 선형 회귀는 error의 평가 기준을 평균 제곱 오차(MSE)로 삼기 때문에 cost function을 아래와 같이 둡니다. (사실 선형 회귀의 error 기준은 MSA 등 다른 것도 있습니다. 링크한 게시글을 참고해보세요. https://heartbeat.comet.ml/5-regression-loss-functions-all-machine-learners-should-know-4fb140e9d4b0)

각 그래프의 예측된 값과 정답의 차이를 제곱한 것을 다 더한 후, 개수만큼 나누어주면 차이의 평균을 구할 수 있습니다. (제곱을 하는 이유는 마이너스 값을 상쇄하기 위해서입니다.)


cost가 가장 작을 때의 W, b 파라미터를 찾는 것이 선형회귀 문제의 솔루션이 됩니다. 이때 W, b 값을 우리가 직접 찾는 것은 아니고, 머신이 스스로 찾아가게 되는 거죠. 때문에 선형 회귀 문제의 Goal을 말하자면 'minimize cost(W,b)'라고 할 수 있습니다.
이해를 쉽게 하기 위하여 H(x)=Wx로 단순화하여 위 식에 대입하면 아래와 같은 식을 얻을 수 있습니다.

위 식에서 x, y는 수치를 알고 있는 상수이기 때문에 cost 함수는 결국 W를 변수로 갖는 아래와 같은 이차 함수의 꼴을 갖는 것을 예측할 수 있습니다. (cost 함수는 W를 변수로 하는 함수라는 것을 주의해야 합니다!)
# 코딩으로 구현하기: 평균 제곱 오차(MSE)
아래의 포스트에서 이를 자세히 다루었습니다.
https://classic-griver.tistory.com/154
[모두의 딥러닝] #2. 선형 회귀(Linear regression) 코딩으로 구현하기
'모두의 딥러닝' 개정 2판의 예제 코드를 이용하여 공부한 글입니다. 앞서서 선형 회귀의 이론에 대해 자세히 공부해보았습니다. 해당 글은 바로 아래에 링크해두었습니다. 2021.12.31 - [개인 공부/
classic-griver.tistory.com
# 최소제곱법(least squares method)
위의 평균제곱오차(MSE) 공식의 변수 a, b에 대해 각각 편미분한 값이 0인 경우에, a, b의 식을 세울 수 있습니다.
그러니까 최소제곱법은 평균제곱오차(MSE)의 특별한 case를 공식으로 만들어 둔 것이라고 볼 수 있습니다. 증명 과정을 필기로 보여드립니다.

# Gradient descent algorithm(경사 하강 알고리즘)
위에서 특정한 기울기 W와 y절편 b로 예측한 함수에 대해 mse를 계산하는 방법을 알아봤습니다.
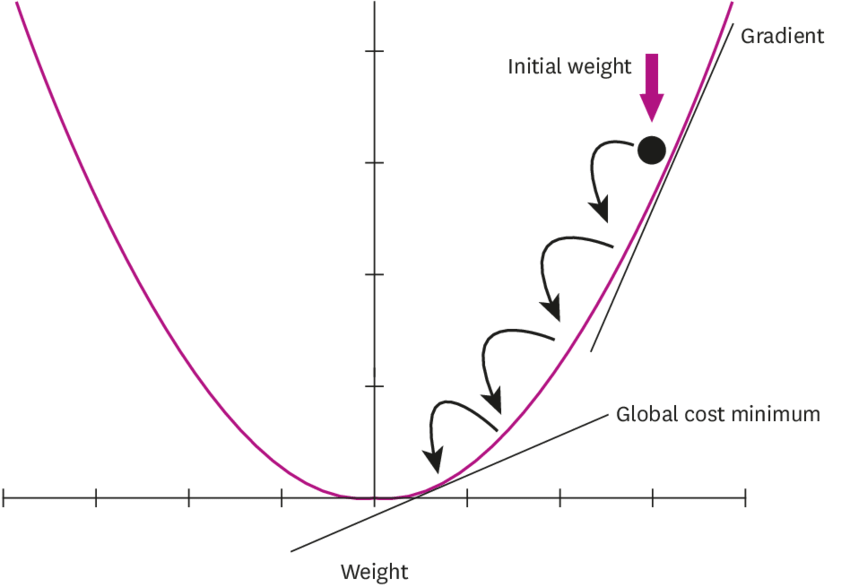
그럼 만약 W, b가 정해지지 않은 상태에서 가장 오차가 작을 때의 W, b 값을 구하고 싶다면 어떻게 해야할까요? 어떻게 머신이 이 그래프를 직접 그려서 최저점을 찾을 수 있을까요? 그 방법 중 하나로 Gradient descent algorithm(경사 하강 알고리즘)이 있습니다.
이 알고리즘은 cost function의 기울기가 0이 되는 곳을 찾는 알고리즘인데요, 이를 위해서 W를 W의 값이 더이상 변하지 않을 때까지 반복하여 기울기가 점점 작아지는 방향으로 이동시키면 됩니다.
경사 하강 알고리즘은 다음과 같이 정의합니다.

좌변의 W는 갱신되는 W(t+1), 우변의 W는 이전의 W(t)라고 봅니다. 그러면 좌변이 우변과 같아질 때, 즉 cost(W)의 W에 대한 편미분이 0이 되는 지점을 찾으면 바로 그게 솔루션이 됩니다.
위 식의 미분을 계산하면 아래와 같은 식이 나옵니다.

따라서 경사 하강법은 반복적으로 기울기를 변화시켜서 최소점을 찾아내는 것으로 그 과정은 아래와 같습니다.

1. a1에서 미분을 구합니다.
2. 구해진 기울기의 반대 방향(+면 -로)으로 얼마 이동시킨 a2에서 미분을 구합니다.
3. 위에서 구한 미분 값이 0이 아니면 위 과정을 반복합니다.
4. 결국 기울기가 0인 한 점 m으로 수렴합니다.
위의 2번 과정에서 상당히 애매한 표현이 등장합니다. '얼마 이동'이라는 표현인데요, 예리하신 분은 여기서 갸우뚱?하셨을 수도 있습니다. 적절한 거리만큼이 아니라 너무 멀리 이동을 시킬 경우에는 a 값이 한 점으로 모이지 않고 발산해버릴 수도 있습니다. 이때 이동 거리를 정해주는 것이 학습률(learning rate)입니다. 딥러닝에서 이 학습률의 값을 적절하게 바꾸면서 최적의 학습률을 찾는 것은 중요한 최적화 과정 중 하나입니다.
그럼 경사 하강법은 '오차의 변화에 따라 이차 함수 그래프를 만들고 적절한 학습률을 설정해 미분 값이 0인 지점을 구하는 것'이라고 말할 수 있습니다.
이때 최대/최소, 즉 optimal 문제의 솔루션을 구하기 위해서는 해당하는 function의 미분값이 0이 되는 지점을 찾으면 되는 거구나!라고 생각하실 수도 있을텐데 아쉽게도 그건 아닙니다. 왜냐하면 최대/최소 문제를 풀 때 유념해야하는 convex function에 대한 논의가 필요하기 때문이죠.
# Convex function
우리가 앞서 풀이한 이차함수의 경우는 언제나 항상 극점이 하나인, 즉 Global minimum을 갖는 Convex function이기 때문에 미분값이 0인 지점이 단 하나이며 그게 바로 솔루션이 됩니다.

convex function를 한국어로 표현하면 볼록 함수 정도로 표현할 수 있습니다. 이런 그래프에서는 어느 점을 잡더라도 항상 단 하나의 unique한 최소값으로 향하게 되죠. 따라서 미분하여 0이 되는 지점을 구하여 답을 내면 됩니다.
그러나 그런 함수는 매우 특별한 경우로 대개는 그렇지 않습니다. 보통은 Non convex function입니다.

이런 함수의 경우에는 local minimum(국소적 최소점)이 여러 개 존재하여 언제나 global minimum을 향한다고 보장할 수 없습니다. 그렇기에 미분값=0을 찾는 게 언제나 적용되는 것은 아닌 것을 알고 있어야합니다.
convex function에 대한 더 자세한 설명은 이 글에 상세히 나와있으니 참고하시길 바랍니다.(http://sanghyukchun.github.io/63/)
# 코딩으로 구현하기: 단순 선형 회귀 경사 하강법
아래의 포스트에서 이를 자세히 다루었습니다.
https://classic-griver.tistory.com/154
[모두의 딥러닝] #2. 선형 회귀(Linear regression) 코딩으로 구현하기
'모두의 딥러닝' 개정 2판의 예제 코드를 이용하여 공부한 글입니다. 앞서서 선형 회귀의 이론에 대해 자세히 공부해보았습니다. 해당 글은 바로 아래에 링크해두었습니다. 2021.12.31 - [개인 공부/
classic-griver.tistory.com
# 3.2 다중 선형(multiple linear regression) 회귀
종속 변수 y에 여러 개의 독립 변수 x1, x2, x3, ... 가 영향을 미치는 상황을 multi-variable를 다루는 문제라고 합니다. 예를 들어, 한 학생의 quiz 1, quiz 2, midterm 세 점수를 사용하여 final 점수를 예측해내는 경우가 있습니다.
위에서 다룬 simple linear regression과 크게 다르지 않습니다. 가설을 설정하고 가설에 대한 cost function을 만들면 아래와 같습니다.


input의 개수가 많아질 수록 수식을 작성하기에 너무 힘들어지기 때문에 matrix를 이용하여 간단히 표현합니다.


그 다음은 모두 단순 선형 회귀와 동일합니다. 그리고 실제로 프로그래밍에 도입할 시, 다중 선형 회귀 식인 H(X)=XW를 사용하면 두 경우 모두 일반화하여 적용할 수 있습니다.
# 코딩으로 구현하기: 다중 선형 회귀 경사 하강법
https://classic-griver.tistory.com/154
[모두의 딥러닝] #2. 선형 회귀(Linear regression) 코딩으로 구현하기
'모두의 딥러닝' 개정 2판의 예제 코드를 이용하여 공부한 글입니다. 앞서서 선형 회귀의 이론에 대해 자세히 공부해보았습니다. 해당 글은 바로 아래에 링크해두었습니다. 2021.12.31 - [개인 공부/
classic-griver.tistory.com
# 정리
선형 회귀란 임의의 직선을 그어 이에 대한 평균 제곱 오차(MSE)를 구하고, 이 값을 가장 작게 만들어 주는 최적 파라미터를 찾아가는 작업입니다.
선형 회귀 문제의 풀이 단계는 이렇습니다.
1. 가설 설정 - Linear Regression!
2. Cost function 디자인
3. Gradient descent 알고리즘을 통해 모델의 파라미터인 W, b 구함
'Study > AI' 카테고리의 다른 글
| [선형대수] 행렬과 벡터의 차이 + 성분곱과 행렬곱, 벡터곱 (2) | 2022.01.16 |
|---|---|
| [모두의 딥러닝](keras) #2-2. 선형 회귀(Linear regression) 코딩으로 구현하기 (4) | 2022.01.05 |
| [모두의 딥러닝] #1. 딥러닝 프로그램의 작업 환경 만들고 구조 알아보기 + 기초 수학 (2) | 2021.12.28 |
| #2.2 인공지능 개요 | 인공지능 (0) | 2021.11.09 |
| #2.1 강의 OT | 인공지능 (0) | 2021.11.09 |



