'모두의 딥러닝' 개정 2판 + 세종대학교 최유경 교수님의 머신러닝(2021) + alpha 로 공부한 글입니다.
# 딥러닝의 동작 원리
# 5장: 로지스틱 회귀(logistic regression)
로지스틱 회귀(logistic regression)는 참과 거짓 중에 하나를 내놓는 과정입니다. 그리고 이 과정이 바로 딥러닝의 토대를 이룹니다.
# 5.1.1 로지스틱 회귀(logistic regression)의 정의
독립변수와 종속변수의 관계를 좌표에 나타냈을 때, 직선으로 그래프가 표시되는 경우에는 선형 회귀를 사용하는 것이 적절했습니다. 그러나 독립변수에 따라 0 아니면 1, O 아니면 X 등 두 개의 종속변수 값으로만 나타나는 경우도 있습니다. 예를 들어 다음과 같은 경우가 있을 것입니다.
| 공부한 시간 | 2 | 4 | 6 | 8 | 10 | 12 | 14 |
| 합격 여부 | 불 | 불 | 불 | 합 | 합 | 합 | 합 |
이 점들은 1과 0 사이의 값이 존재하지 않으므로 직선으로 그리는 것은 사실상 불가합니다. 이런 범주형 숫자 데이터에는, 즉 분류 문제는 Linear regression을 이용한 풀이가 불가합니다. 때문에 S자 곡선으로 그려져야 합니다.
# 5.2 시그모이드(sigmoid) 함수 = 로지스틱 함수(logistic function)
S자 형태의 그래프로 그려지는 함수가 바로 시그모이드 함수입니다. 시그모이드 함수의 공식과 그래프의 모양은 아래와 같습니다.
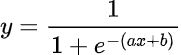

시그모이드 함수의 공식에 선형회귀와 동일하게 ax+b가 있습니다.
a가 의미하는 것은 그래프의 경사도입니다. a 값이 커지면 경사가 급해지고, a 값이 작아지면 경사도 작아집니다.
a는 지수이고 그 앞에 -가 붙어있습니다. 따라서 a값이 커질수록 분모가 작아지므로 y값은 커지고, a 값이 작아질수록 분모가 커지므로 y값은 작아집니다.

b가 의미하는 것은 그래프의 좌우 평행이동입니다. b가 커지면 왼쪽으로, b가 작아지면 오른쪽으로 이동합니다. e의 지수를 정리하면 -a(x+b/a)이므로 -b/a만큼 평행이동하고, 따라서 b가 커지면 -방향으로, b가 작아지면 +방향으로 이동합니다.

그래프가 형태가 a, b에 의해 결정되므로 오차도 a, b 값에 따라 달라집니다.
a 값이 작아지면 오차는 무한대로 커지고, a 값이 커지면 오차는 작아집니다.

b 값이 너무 크거나 작으면 오차는 이차 함수 그래프처럼 나타납니다.

# 5.3 오차 공식(Cost function)
그렇다면 a, b 값을 구하는 방법은 무엇일까요? 바로 앞서 배웠던 경사 하강법입니다.
경사 하강법을 사용하기 위해서는 먼저 실제값과 예측값의 차이인 오차 함수(cost function)을 구해야합니다. 그런 다음에 오차가 작은 쪽으로 점점 이동하는 것이죠.
그럼 시그모이드 함수 그래프에서는 어떻게 cost function을 구할 수 있을까요? 시그모이드 함수의 특징을 잘 생각해보면 알 수 있습니다. 시그모이드 함수는 y 값이 0~1 사이의 값을 갖습니다. 따라서 실제 값이 1인데 예측을 0으로 할 때, 실제 값이 0일 때 예측을 1으로 할 때 오차가 커지겠죠. 이 패턴을 공식화할 수 있게 해주는 함수가 로그함수입니다.

-log h
-log h인 파란색 선이 실제 값이 1일 때 사용하는 그래프입니다. 예측 값이 1일 때 오차가 0이고 예측 값이 0에 가까울 수록 오차가 커집니다.
-log (1-h)
-log (1-h)인 빨간색 선이 실제 값이 0일 때 사용하는 그래프입니다. 예측 값이 0일 때 오차가 1이고 예측 값이 1에 가까울 수록 오차가 커집니다.
실제 값이 1일 때와 0일 때를 구분하여 파란 그래프와 빨간 그래프를 사용해야 합니다. 이걸 어떻게 하나의 식으로 표현할 수 있을까요? 실제 값이 1일 때 빨간 그래프가 사라지게 하고, 실제 값이 0일 때 파란 그래프가 사라지게 하면 될 것입니다. 그 공식은 아래와 같습니다.

y가 실제 값이라면 y=0일 때에는 뒤의 함수만, y=1일 때에는 앞의 함수만 남겠죠. 따라서 실제 값에 따라 빨간 그래프와 파란 그래프를 사용할 수 있습니다. 이 함수가 cost function이 되겠습니다.
# 5.4 코딩으로 구현하기
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
data = [[2,0],[4,0],[6,0],[8,1],[10,1],[12,1],[14,1]]
x_data = [i[0] for i in data] # 공부한 시간 데이터
y_data = [i[1] for i in data] # 합격 여부
plt.scatter(x_data,y_data)
plt.xlim(0,15) # x축은 0~15
plt.ylim(-0.1,1.1) # y축은 -0.1~1.1
plt.scatter(x_data,y_data)
plt.xlim(0,15) # x축은 0~15
plt.ylim(-0.1,1.1) # y축은 -0.1~1.1
def sigmoid(x): # sigmoid라는 이름의 함수 정의
return 1/(1+np.e**(-x)) # sigmoid 함수 식
# 경사 하강법 시행
for i in range(2001):
for x_data, y_data in data:
# a에 관한 편미분. 앞서 정의한 sigmoid 함수 사용
a_diff = x_data*(sigmoid(a*x_data+b)-y_data)
# b에 관한 편미분
b_diff = sigmoid(a*x_data+b)-y_data
# a를 업데이트 하기 위해 a_diff에 학습률 lr 곱한 값을 a에서 뺀다.
a = a - lr*a_diff
# b를 업데이트 하기 위해 b_diff에 학습률 lr 곱한 값을 b에서 뺀다.
b = b - lr*b_diff
if i%1000 == 0:
print("epoch=%.f, 기울기=%.04f, 절편=%.04f, a편미분=%.04f, b편미분=%.04f" %(i,a,b,a_diff,b_diff))
# 앞서 구한 기울기와 절편 이용해 그래프 그리기
x_data = [i[0] for i in data] # x_data와 y_data에 값 다시 넣어줘야 함
y_data = [i[1] for i in data]
plt.scatter(x_data, y_data)
plt.xlim(0,15)
plt.ylim(-.1,1.1)
x_range = (np.arange(0,15,0.1)) # 그래프로 나타낼 x 값의 범위 정하기
plt.plot(np.arange(0,15,0.1),np.array([sigmoid(a*x+b) for x in x_range]))
plt.show()
x_data
# 5.5 세 개 이상의 입력 값
위에서는 두 개의 입력 값이 있을 때를 다루어보았습니다. 여기에 입력 값이 추가되어 세 개 이상의 입력 값을 다룬다면, 시그모이드 함수를 더이상 사용하지 못하고 소프트맥스(softmax) 함수를 사용해야 합니다. 이는 '12장 다중 분류 문제 해결하기'에서 다룰 예정입니다.
# 5.6 로지스틱 회귀에서 퍼셉트론으로
입력 값을 통해 출력 값을 구하는 함수 y는 아래와 같이 표현됩니다.

x 값들을 입력 값이라고 하고, y를 출력 값이라고 합니다.
x 값들이 입력되면, 각각 가중치 a1, a2를 만나고 여기에 b 값을 더한 것이 시그모이드 함수를 거쳐 1이나 0의 출력 값 y를 출력합니다. 이 과정을 퍼셉트론 방식으로 표현한 것이 아래의 그림입니다.

이런 퍼셉트론 개념이 인공 신경망, 오차 역전파 등을 거쳐서 현재의 딥러닝에 이르게 되었습니다.
'Study > AI' 카테고리의 다른 글
| [부스트코스 코칭스터디 AI Basic 1기] #1-3. 파이썬 기초 문법Ⅱ (0) | 2022.01.24 |
|---|---|
| [모두의 딥러닝](Pytorch) #4. XOR 문제에서 발견한 퍼셉트론의 한계 + 다층 퍼셉트론(신경망)을 통한 해결 (4) | 2022.01.20 |
| [부스트코스 코칭스터디 AI Basic 1기] #1-1. 파이썬/AI 개발환경 준비하기 (0) | 2022.01.16 |
| [모두의 딥러닝](Pytorch) #2-3. 선형 회귀(Linear regression) 코딩으로 구현하기 (0) | 2022.01.16 |
| [선형대수] 행렬과 벡터의 차이 + 성분곱과 행렬곱, 벡터곱 (2) | 2022.01.16 |

